Mainnavigation
Subnavigation
BORDER
Pagecontent
Least Squares Deep Fade Filter Design
These SatLab plots comes from testing a least squares filter to cope with time delay and doppler during deep fade. These plots are from the period of maximum change in the rate of deep fade.
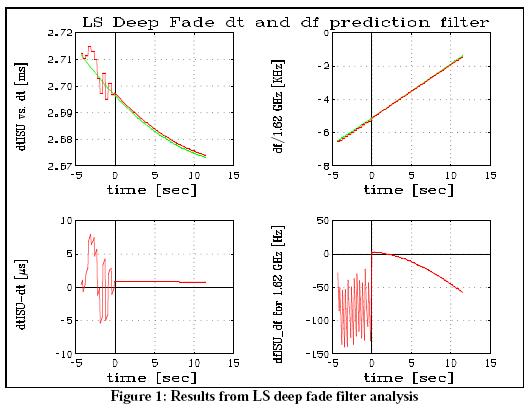
% demo Deep Fade Filter
%
% The requirements for handsets for GMPCS satellite systems is
% that they do not loose synchronization during short time
% deep fades. They need to include a filter to predict time
% delay and doppler during the time of a deep fade where
% synchronization signals are not received from a satellite.
% This filter needs to meet the requirements after receiving
% synchronization time delay and doppler synchronization
% data for a minimum specified time.
%
% In this demo a least squares filter is designed and analyzed
% that easily meets the requirements to predict dt and df
% for 128 frames after receiving synchronization data from
% a satellite for 48 frames, with associated measurement
% errors. The results are for the time of maximum rate of
% change of df.
% SatLab demo: Horst C. Salzwedel
help demoDeepFadeFilter
% Initialization
removeAll;
clearGraphic();
clear;
loadreplaceAll("./IRsingle.data");
setSimEpoch(2002,3,26,11,58,54.91185); %0 sec
setSimTime(0);
g = GeoPosition(3);
g = g(1:2,:);
lat0 = g(1,1);
lon0 = g(2,1);
setStationParameter('E1',I_earth,0,lat0*r2d,lon0*r2d,0);
setSimEpoch(2002,3,26,11,58,34.91185); %-20 sec
setSimTime(0);
% L-band Frame length = 90 ms
LBframe = .090;
setSimStepSize(LBframe);
% Minimum Connection Time = 48 L-band frames
mct = 50*LBframe;
% L-band frequency
fLB = 1.62e9;
% Initialization of SV
iSV = 0;
dtsum = 0;
dfsum = 0;
% Initialization of ISU
[d,r,a,e,v] = RelPosition('E1');
dfISU0 = r(2)/cLight*fLB;
dfISU = dfISU0;
dtISU0 = d(2)/cLight;
dtISU = dtISU0;
dtISUcorrection = 0;
dfISUcorrection = 0;
rand("normal");
rand("seed",260342);
sigdtm = 4e-6; %measurement error 4 microseconds
sigdfm = 20; %measurement error 20 Hz
sigdtr = 2e-6; %reporting error 2 microseconds
sigdfr = 9.8; %reporting error 9.8 Hz
% Time delay and doppler frequency prediction filter
% state d [km] state v [km/s] state a [km/s/s]
ifade = 0;
ii = [-48:1:ifade ifade+1:1:ifade+127];
j = 0;
ils = 0;
Ydflast = dfISU;
Ydtlast = 0;
for i = ii,
j = j + 1;
stepSim; %step simulation forward by one L-band frame
% Filter time update
if (i >= ifade)
tt = i*LBframe;
dfISU = Xhat(1) + Xhat(2)*tt;
dtISU = dtISU0 + Xhat(3) + Xhat(1)/fLB*tt + Xhat(2)/(2*fLB)*tt^2;
endif
% Doppler and Time Delay of up/down link
[d,r,a,e,v] = RelPosition('E1');
Mdf(j) = r(2)/cLight*fLB; % store df in array
Mdt(j) = d(2)/cLight; % store dt in array
% Measurement of dt and df by SV
dtsum = dtsum - dtISU + Mdt(j) + sigdtm*rand(1);
dfsum = dfsum - dfISU + Mdf(j) + sigdfm*rand(1);
iSV = iSV + 1;
if (iSV == 4)
DTOA = dtsum/4 + sigdtr*rand(1);
DFOA = dfsum/4 + sigdfr*rand(1);
dtsum = 0;
dfsum = 0;
iSV = 0;
%transmit FTOA and DFOA to ISU
dtISUcorrection = DTOA;
dfISUcorrection = DFOA;
if (i < ifade)
ils = ils + 1;
if ils > 12
ils = 1;
endif
Ydf(ils) = Ydflast+DFOA;
Ydflast = Ydf(ils);
Ydt(ils) = Ydtlast+DTOA;
Ydtlast = Ydt(ils);
Tls(ils) = (i - 1.5)*LBframe;
% ISU control loop filter
dfISU = dfISU + dfISUcorrection;
dtISU = dtISU + dtISUcorrection;
endif
endif
% Do least square estimation for last time before fade
if (i == (ifade-1))
% Least squares solution
%
% [ ydt ] = [ t/f t^2/(2f) 1 ] [ a0 ]
% [ ydf ] [ 1 t 0 ] [ a1 ]
% [ b0 ]
% where
% df = a0 + a1*t
% dt = b0 + a0/f*t + a1/(2f)*t^2
%
% form matrix A
A = [ Tls/fLB Tls.*Tls/(2*fLB) ones(size(Tls));
ones(size(Tls)) Tls zeros(size(Tls)) ];
YY = [Ydt
Ydf];
Xhat = A\YY;
tt = i*LBframe;
dtISU = dtISU0 + Xhat(3) + Xhat(1)/fLB*tt + Xhat(2)/(2*fLB)*tt^2;
endif
% Per frame correction of dt and df
MdtISU(j) = dtISU;
MdfISU(j) = dfISU;
endfor
erase
title('LS Deep Fade dt and df prediction filter')
window('221')
plot(ii'*LBframe,Mdt*1000,'grid','green',
ii'*LBframe,MdtISU*1000,'red','grid')
xlabel('time [sec]'); ylabel('dtISU vs. dt [ms]')
window('223')
plot(ii'*LBframe,(MdtISU-Mdt)*1000000,'grid','red')
xlabel('time [sec]');
ylabel('dtISU-dt (ms)',
'll ll sGls')
window('222')
plot(ii'*LBframe,Mdf/1000,'grid','green',
ii'*LBframe,MdfISU/1000,'red')
xlabel('time [sec]'); ylabel('df/1.62 GHz [KHz]')
window('224')
plot(ii'*LBframe,(MdfISU-Mdf),'grid','red')
xlabel('time [sec]'); ylabel('dfISU-df for 1.62 GHz [Hz]')